- 사람과 사람 간에 의사소통을 하기 위해 언어(한글, 영어 등)가 필요하듯이 컴퓨터도 장비들끼리 의사소통을 할 수 있는 언어가 필요하다. 그 용도로 사용되는 것이 비트와 바이트이다.
2진법
- 우리가 일상에서 사용하는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 총 10개의 기호로 표현하는 것이 10진법이다.
- 하지만 컴퓨터에는 이렇게 많은 숫자가 없다. 오직 0과 1로만 데이터를 표현한다. 이처럼 0과 1로만 표현하는 것을 2진법이라고 한다.
- 컴퓨터는 신기하게도 오로지 0과 1만으로 숫자뿐만 아니라 글자, 사진, 영상, 소리 등을 저장할 수 있다.
- 2진법에서는 두 개의 숫자만 있으므로 각 자릿수가 2의 거듭제곱을 의미한다.
비트(bit), 2진수(binary digit)
- 컴퓨터에서 처리하는 정보의 최소 표현 단위
- 컴퓨터에서 정보를 저장하고 연산을 수행하기 위해 두 가지 값(0과 1)을 기반으로 한 측정 단위
- 2진법에서 하나의 자릿수를 표현하는 단위
- 컴퓨터는 0과 1의 조합으로 수의 계산과 논리 계산을 한다. 이는 비트를 조합해서 하나의 문자나 숫자, 기호 등 우리가 사용하는 일상의 문자나, 기호 표현을 할 수 있다.
- 디지털 데이터를 여러 비트들로 나타냄으로써 두 가지 값만을 가지고도 많은 양의 정보를 저장할 수 있다.
- 컴퓨터는 저장되어 있는 데이터를 수정하기 위해 비트에 수학적 연산을 수행할 수 있다.
비트열
- 하나의 비트는 두 가지의 값(0과 1)만 저장할 수 있다.
- 비트 한 개는 많은 양의 데이터를 나타내기에 턱없이 부족하기 때문에 여러 숫자 조합을 컴퓨터에 나타내기 위한 비트열을 사용한다.
- 바이트는 8개의 비트가 모여 만들어진 것이다.
- 바이트가 모이면 더 큰 단위가 될 수 있다.

| *Sl 접두어 | 전통적 용법 | *이진 접두어 | |||
| KB (킬로바이트) | 1000^1 = 10^3 | KB | 1024^1 = 2^10 | KiB (키비바이트) | 2^10 |
| MB (메가바이트) | 1000^2 = 10^6 | MB | 1024^2 = 2^20 | MiB (메비바이트) | 2^20 |
| GB (기가바이트) | 1000^3 = 10^9 | GB | 1024^3 = 2^30 | GiB (기비바이트) | 2^30 |
| TB (테라바이트) | 1000^4 = 10^12 | TB | 1024^4 = 2^40 | TiB (테비바이트) | 2^40 |
| PB (페타바이트) | 1000^5 = 10^15 | PB | 1024^5 = 2450 | PiB (페비바이트) | 2^50 |
| EB (엑사바이트) | 1000^6 = 10^18 | EB | 1024^6 = 2^60 | EiB (엑스비바이트) | 2^60 |
| ZB (제타바이트) | 1000^7 = 10^21 | ZB | 1024^7 = 2^70 | ZiB (제비바이트) | 2^70 |
| YB (요타바이트) | 1000^8 = 10^24 YB | YB | 1024^8 = 2^80 | YiB (요비바이트) | 2^ 80 |
- SI 접두어 : 10진법을 기반으로, 일상적인 수치와 통계에서 사용된다.
- 이진 접두어 : 2진법을 기반으로, 컴퓨터 과학 및 기술 분야에서 데이터 용량을 정확하게 표현하기 위해 사용된다.
바이트(btye)
- 1바이트는 8비트로 구성된 비트 집단(2^8)이다.
- 왜 8비트일까 : 영문 알파벳의 대소문자(26 + 26) + 숫자(10) + 특수문자(66) + 국가 및 회사별 추가적인 문자(128) = 256 = 2^8
- 2^7로 표현된 코드로 대표적인 것이 아스키코드이다.
- 왜 8비트일까 : 영문 알파벳의 대소문자(26 + 26) + 숫자(10) + 특수문자(66) + 국가 및 회사별 추가적인 문자(128) = 256 = 2^8
- 숫자나 글자, 로마자 등을 표현하기 위한 정보의 양을 나타내는 기본 단위
문자의 표현
- 문자를 숫자로 표현할 수 있도록 정해진 약속(표준)이 있다.
- 그중 하나는 미국정보교환표준부호 ASCII(아스키코드, American Standard Code for Information Interchange)이다.
- 아키코드는 총 128개의 부호로 정의되어 있다.

- 이 외에도 Unicode 라는 표준에서는 더 많은 비트를 사용하여 더 다양한 다른 문자들도 표현가능 하도록 지원하고 있다.
그림, 영상, 음악의 표현
- 문자와 같이 그림도 역시 숫자로 표현할 수 있다.
- 우리가 스크린을 통해 보는 그림을 자세히 살펴보면 수많은 작은 점들이 빨간색, 초록색, 파란색을 띠고 있다. 이런 작은 점을 픽셀이라고 부른다.
- 각각의 픽셀은 세 가지 색을 서로 다른 비율로 조합하여 특정한 색을 갖게 된다. 이 숫자들을 표현하는 방식을 RGB(Red, Green, Blue)라고 한다.
- 영상 또한 수많은 그림을 빠르게 연속적으로 이어 붙여놓은 것이기 때문에 숫자로 표현이 가능하다.
- 음악도 마찬가지로 각 음표를 숫자로 표현할 수 있다.
픽셀
[Android] px(pixel), dp(dip), sp
픽셀(pixel, px)화소라고도 하며, 디지털 이미지를 나타내는 데 사용되는 최소 단위이다.해상도와도 관련이 있는데, 동일한 이미지라 하더라도 픽셀의 수가 많은 것이 해상도가 더 높다.오른쪽 그
dev-baik.tistory.com
자료형
[Kotlin] 자료형(기본형, 참조형), Call by Value, Call by Reference
자료형자바의 자료형은 크게 기본 자료형과 참조 자료형으로 나뉜다. 하지만 코틀린에서는 자바와 달리 null 값을 가질 수 있기 때문에 기본 자료형을 지원하지 않는다.코틀린은 기본 자료형을
dev-baik.tistory.com
음수 표현법
1. 부호 절댓값 (Sign-Magnitude)
- 최상위 비트(가장 왼쪽의 비트, Most Significant Byte, MSB)를 이용하는 방법으로, 최상위 비트가 0인 경우는 양수를 나타내고, 1인 경우는 음수를 나타내어 숫자의 부호를 결정한다.
- 예시: 5 = 0000 0101, -5 = 1000 0101
- 최상위 비트만 고려해 주면 되기 때문에 사람 입장에서는 직관적이다.
- +0과 -0 둘 다 존재하기 때문에 둘 다 0으로 인식하도록 설정해야 한다.
- 뺄셈을 위해 각 수가 음수인지 정수인지에 따라 고려해야 할 사항이 많아져 회로가 복잡해지고 복잡성이 증가한다.
- 두 수의 최상위 비트가 같다면, 결괏값의 최상위 비트도 같다.
- 예시: 0001 0111(23) + 0001 1111(31) = 0011 0110(54), 1001 0111(-23) + 1001 1111(-31) = 1011 0110(-54)
- 두 수의 최상위 비트가 다르면, 절댓값이 큰 수가 첫 번째 수가 되도록 하여 숫자의 부호를 결정한다.
- 예시: 1001 0111(-23) - 0001 1111(+31) → 0001 1111(+31) - 1001 0111(-23) = 0000 1000(8)
- 두 수의 최상위 비트가 같다면, 결괏값의 최상위 비트도 같다.
2. 보수 (Complement)
- 보수 : 각 자리의 숫자의 합이 어느 일정한 수가 되게 하는 수 = 현재의 숫자에서 자릿수가 한 단계 올라가기 위한 수
- r 진법에서 n 에 대한 r 의 보수 : 어떤 수에 대해 음수가 되지 않는 선에서의 n 의 최소 제곱수가 되도록 만드는 수
- 예시: 10진법에서 3에 대한 10의 보수 = 10 - 7 = 3, 723에 대한 10의 보수 = 1000 - 723 = 277
- 예시: 8진법에서 723에 대한 8의 보수 = 1000₍₈₎(8³, 512) - 723₍₈₎(467) = 55₍₈₎(45)
- r 진법에서 n 에 대한 (r - 1)의 보수 : *최댓값 - n
- 최댓값 : 그 자리에서 가질 수 있는 최댓값, 한 자리의 최댓값 = r - 1
- 예시: 10진법에서 723에 대한 9의 보수 = 999 - 723 = 276
- 예시: 8진법에서 723에 대한 7의 보수 = 777₍₈₎ - 723₍₈₎ = 54₍₈₎
- r 진법에서 n 에 대한 r 의 보수 : (r - 1)의 보수 + 1
- 예시: 10진법에서 723에 대한 10의 보수 = 276 + 1 = 277
- 예시: 8진법에서 723에 대한 8의 보수 = 54₍₈₎ + 1₍₈₎ = 55₍₈₎
- 부호 절댓값과 달리, 이를 통해 음수와 양수에 관계없이 일관되게 덧셈만으로 결과를 얻을 수 있다.
- 예시: -23 + 31 = {(100-23) + 31} - 100 = {77+31} - 100 = 108 - 100 = 8
- 이를 약간 변형하여 보수만 구하는 방식으로 바꿀 수 있다. 이전에는 보수를 구하기 위해 100을 더한 후 다시 빼는 방식이었지만, 이제는 보수만 구하고 다시 빼지 않는 것이다.
- 예시: {(100 - 23)+31} = {77+31} = 108
- 여기서 가장 왼쪽 값 1은 올림으로 발생한 수이기 때문에 버린다. 이를 최상위 비트에서 자리 올림이 되었다는 의미로 캐리 발생이라고도 한다. 이때 자리 올림 즉, 캐리가 발생할 경우 양수라는 의미이고, 캐리가 발생하지 않는 경우 음수라는 의미이다.
- 예시: 108에서 1을 버린 08, 즉 8이 정답이 된다. (올림이 발생한 경우)
- 캐리가 발생하지 않은 경우에는 해당 수의 보수를 구한 후, 그 값에 음수 부호를 붙이면 된다.
- 예시: -31 + 23 = {(100 - 31} + 23} = 69 + 23 = 92 → 100 - 92 = 8 → -8
- 두 수 모두 음수인 경우 예시: -23 - 31 = (100 - 23) + (100 - 31) = 146 (올림 발생) → 46 (올림 발생하지 않음) → 100 - 46 = 54 → -54
- 9의 보수 예시: 23 - 31 = 23 + (99 - 31) = 91 (올림 발생하지 않음) → 99 - 91 = 8 → -8
3. 1의 보수 (One's Complement)

- 2진법에서 3에 대한 1의 보수 = 1111 1111₍₂₎ - 0000 0011₍₂₎ = 1111 1100₍₂₎ = -3
- 비트를 반전(NOT) 연산만으로는 음수 값을 얻을 수 있다.
- 최상위 비트의 성질이 유지된다.
- 덧셈만으로 뺄셈을 구현할 수 있어 비교적 회로가 단순하다.
- 캐리가 발생하는 경우를 처리해주어야 한다.
- -0과 +0을 모두 인지할 수 있도록 처리해주어야 한다.
4. 2의 보수 (Two's Complement)
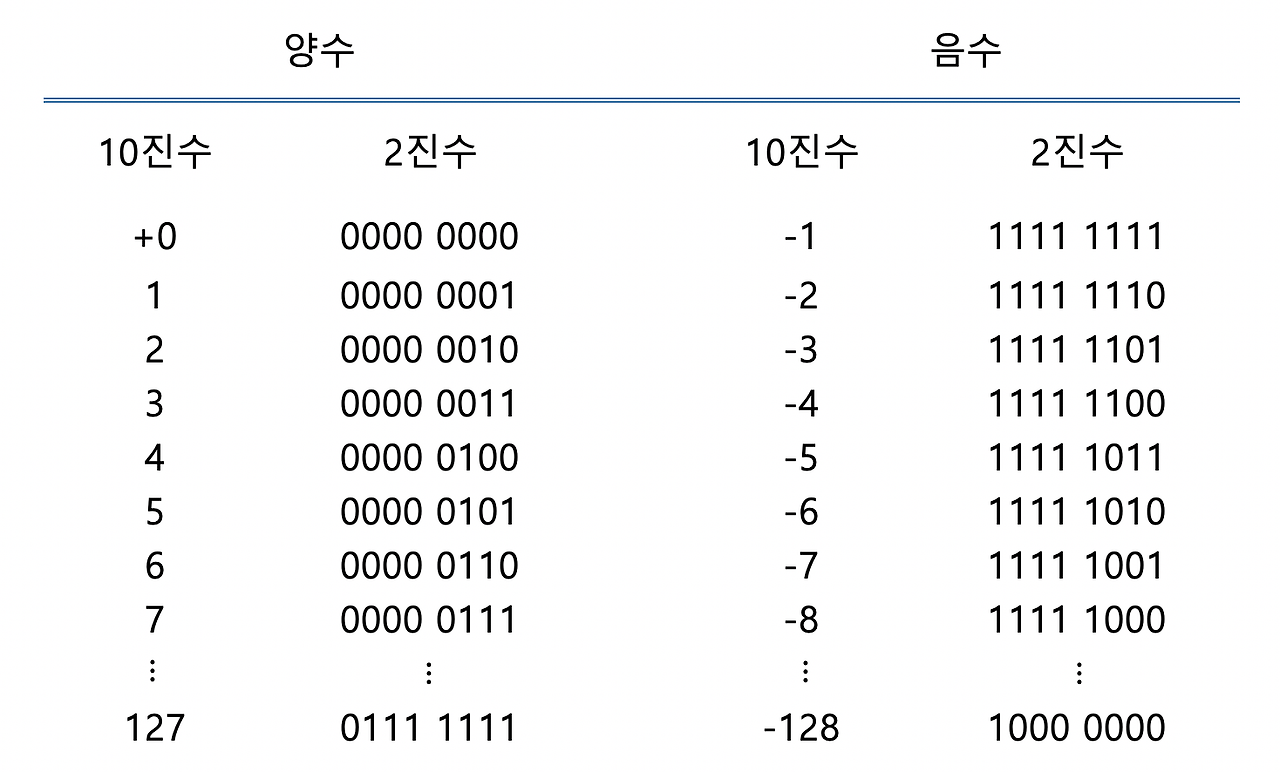
- -0을 없애기 위해 음수 영역의 각 수를 -1씩 조정하여 대응시킨다.
- 2의 보수는 1의 보수에 + 1 을 하면 음수값을 얻을 수 있다.
- r 진법에서 n 에 대한 r 의 보수는 (r - 1)의 보수 + 1 이다.
- 1, 2, 3은 모두 같은 의미이다.
- 예시: -23 + 31 = 1110 1001 + 0001 1111 = 0000 1000 = 8 (올림이 발생하더라도 올바른 값이 나온다)
- 최상위 비트 성질이 유지된다.
- 덧셈만으로 뺄셈을 구현할 수 있어 회로가 단순해진다.
- 1의 보수의 단점을 모두 해결할 수 있다.
- 다른 방법 : 1. 뒤에서부터 처음 만나는 1까지는 적는다 → 2. 나머지는 0과 1을 반전시킨다.
비트 연산
- 정수형 변수를 사람이 사용하는 10진법으로 연산하는 대신 2진법인 비트 단위로 연산할 수 있는 기능
bitwise shift operators (비트를 밀어주는)
- shl(shift left) : 부호 비트를 제외한 모든 비트를 좌측으로 밀어주는 기능
- shr(shift right) : 부호 비트를 제외한 모든 비트를 우측으로 밀어주는 기능
- ushr(unsigned shift right) : 부호 비트를 포함한 모든 비트를 우측으로 밀어주는 기능
bitwise operators (비트를 조작하는)
- and : 원본과 비교하여 둘 다 1인 자리만 1로 반환
- 비트를 확인하는 용도 (원하는 위치에만 1을 넣어 확인)
- 비트를 clear 하는 연산 (원하는 자리에 0을 넣어 clear)
- or : 원본과 비교하여 하나라도 1인 자리면 1로 반환
- 비트의 set연산, 즉 비트 값을 1로 설정하고 싶을 때 (1을 넣어주면 1로 set 가능)
- xor : 비트가 같으면 0, 다른 자리는 1로 반환 (비트별로 동일한지 사용)
inv() (비트를 반전하는)
- 비트를 모두 반전시키는 역할
모두를 위한 컴퓨터 과학 (CS50 2019)
부스트코스 무료 강의
www.boostcourse.org
모두를 위한 컴퓨터 과학 (CS50 2019)
부스트코스 무료 강의
www.boostcourse.org
비트(bit)와 바이트(Byte)란?왜 8비트는 1바이트인가? 킬로바이트(kilobyte) 메가바이트(megabyte) 기가
안녕하세요. 비티샘입니다. 오늘은 우리의 이진법 체계에서 자주 사용하는 비트에 대해 알아보겠습니다. C...
blog.naver.com
바이트 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 스토리지 크기가 늘어남에 따라 10진, 2진 해석의 차이가 커진다. 이를 백분율로 비교 차트이다. 바이트(byte)는 컴퓨터의 기억장치의 크기를 나타내는 단위로 자
ko.wikipedia.org
[Kotlin] 비트연산 설명 & 예제
비트연산 정수형 변수를 사람이 사용하는 10진법으로 연산하는 대신 2진법인 비트 단위로 연산할 수 있는 기능 실무에서는 비트연산을 계산에는 거의 사용하지 않음 2진법을 이요한 연산 최적화
hkoonsdiary.tistory.com
2진수의 수와 음수 표현법 [1의 보수와 2의 보수]
안녕하세요. 오늘은 프로그래밍이 아닌 컴퓨터의 연산에 대해 이해해보고자 합니다. 우리가 흔히 프로그래밍을 할 때는 그나마 사람에 가까운 언어로 된 고급언어들로 작성을 하지만 실제 컴퓨
st-lab.tistory.com
보수란? - 1의 보수, 2의 보수
안녕하세요. 취업한 공대누나입니다. 기초적인 논리 회로를 많이 까먹어서 논리회로를 복습해보고자 합니다. 오늘은 보수의 개념에 대해 알아보도록 하겠습니다. 1. 보수란? 우선 보수란 각 자
gdnn.tistory.com
'안드로이드 > etc.' 카테고리의 다른 글
| [CS] 멀티 태스킹(Multi Tasking), 멀티 프로세싱(Multi Processing), 멀티 프로세스(Multi Process), 멀티 스레드(Multi Thread) (0) | 2024.12.12 |
|---|---|
| [CS] 블록체인(Blockchain) (0) | 2024.11.25 |
| [Kotlin] 에러(Error)와 예외(Exception) (0) | 2024.11.20 |



