정렬 (sorting)
- 어떤 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 것
val dataList = (0..99).shuffled().take(10).toIntArray()
println("Before sorting: ${dataList.joinToString(", ")}")
선택 정렬 (Selection Sort)
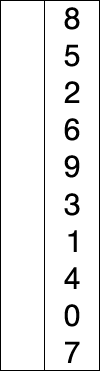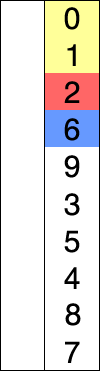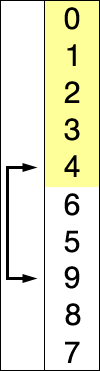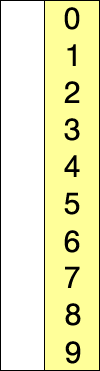
1. 주어진 리스트 중에 최소값을 찾는다.
2. 해당 최소값을 데이터 맨 앞에 위치한 값과 교체한다.
3. 맨 처음 위치를 뺀 나머지 데이터를 같은 방법으로 교체한다.
| 시간 복잡도 | average, worst : O(N²) (구현이 간단하지만 비효율적) |
| 공간 복잡도 | 제자리(In-place) 알고리즘 (기존 배열 외에 추가적인 메모리를 거의 사용하지 않는다) |
| 안전성 | 불안전정렬 (정렬을 수행할 때 동일한 값을 가진 원소들의 원래 순서가 유지되지 않는다) |
fun selectionSort(arr: IntArray): IntArray {
for (i in 0 until arr.lastIndex) {
var min_idx = i
for (j in i + 1..arr.lastIndex) {
if (arr[min_idx] > arr[j]) {
min_idx = j
}
}
arr[min_idx] = arr[i].also { arr[i] = arr[min_idx] }
}
return arr
}
val sortedList = selectionSort(dataList)
println("After sorting: ${sortedList.joinToString(", ")}")
삽입 정렬 (Insert Sort)
1. 삽입 정렬은 두 번째 인덱스부터 시작한다.
2. 해당 인덱스(key 값) 앞에 있는 데이터(B)부터 비교해서 key 값이 더 작으면, B 값을 뒤 인덱스로 복사한다.
3. 이를 key 값이 더 큰 데이터를 만날때까지 반복, 그리고 큰 데이터를 만난 위치 바로 뒤에 key 값을 이동한다.
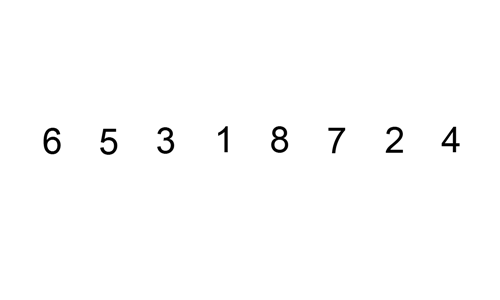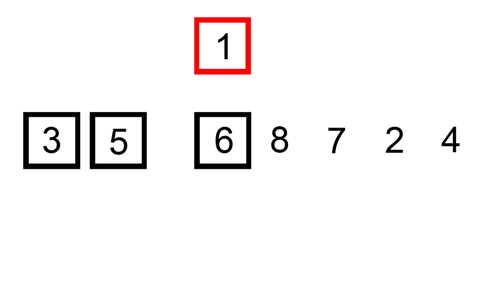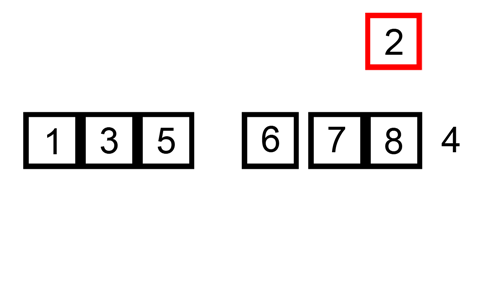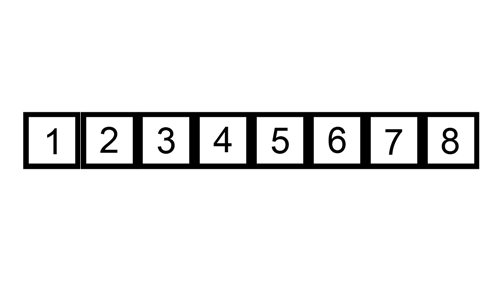
| 시간 복잡도 | - average : O(N²) - worst(모든 원소가 이미 정렬되어있는 경우) : O(N) (이미 정렬이 대부분 되어있는 경우 효율적) |
| 공간 복잡도 | 제자리(In-place) 알고리즘 |
| 안전성 | 안전정렬 : 비교대상의 원소가 새로운 원소보다 클 때만 한자리 뒤로 이동시키므로 동일한 원소의 우선순위는 처음 정렬과 동일하게 유지된다. |
fun insertionSort(arr: IntArray): IntArray {
for (i in 0 until arr.lastIndex) {
for (j in i + 1 downTo 1) {
if (arr[j - 1] > arr[j]) {
arr[j - 1] = arr[j].also { arr[j] = arr[j - 1] }
} else {
break
}
}
}
return arr
}
val sortedList = insertionSort(dataList)
println("After sorting: ${sortedList.joinToString(", ")}")fun insertionSort(arr: IntArray): IntArray {
for (i in 0 until arr.lastIndex) {
var index = i
var temp = arr[i]
while (index > 0 && arr[index - 1] > temp) {
arr[index] = arr[index - 1]
index--
}
arr[index] = temp
}
return arr
}
val sortedList = insertionSort(dataList)
println("After sorting: ${sortedList.joinToString(", ")}")
버블 정렬 (Bubble Sort)
- 인접한 두 원소를 비교해 나가며 가장 큰 원소를 끝으로 보내는 과정을 N-1 번 반복하는 알고리즘
- 선택정렬과 유사하게, N-1 번 부터 1 번까지의 자리에 대하여 남아있는 수들 중 가장 큰 수를 각 자리로 보낸다.
- 이 때, 버블정렬은 남아있는 수들 중 가장 큰 수를 인접한 두 수를 비교해가며 찾는다.

| 시간 복잡도 | average, worst : O(N²) (구현이 간단하고, 코드가 직관적인다) |
| 공간 복잡도 | 제자리(In-place) 알고리즘 |
| 안전성 | 안전정렬 (동일한 값을 가지는 원소들의 본래 순서가 유지된다) |
fun bubbleSort(arr: IntArray): IntArray {
for (i in 0 until arr.lastIndex) {
var swap = false
for (j in 0 until arr.lastIndex - i) {
if (arr[j] > arr[j + 1]) {
arr[j] = arr[j + 1].also { arr[j + 1] = arr[j] }
swap = true
}
}
if (!swap) break
}
return arr
}
val sortedList = bubbleSort(dataList)
println("After sorting: ${sortedList.joinToString(", ")}")
퀵 정렬 (Quick Sort)
- pivot 을 설정하고 이를 올바른 위치로 이동시킨 후, 피벗을 기준으로 나머지 원소들을 두 개의 배열로 분할하고, 각 부분을 재귀적으로 정렬하여 전체 배열을 정렬하는 알고리즘

| 시간 복잡도 | - average : O(N log N) - worst : 배열이 이미 정렬되어있는 경우, pivot 이 가장 크거나 작은 값이 되면, 한 쪽 배열이 비어있거나 원소가 하나만 남게 되어 재귀 호출의 깊이가 N 에 이르게 된다. 각 단계에서 비교 연산이 평균적으로 N 번 수행되므로, 총 연산 횟수는 O(N²) 이다. |
| 공간 복잡도 | 제자리(In-place) 알고리즘 |
| 안전성 | 불안전정렬 |
fun quickSort(arr: IntArray, left: Int, right: Int): IntArray {
if (left < right) {
val pivot = partition(arr, left, right)
quickSort(arr, left, pivot - 1)
quickSort(arr, pivot, right)
}
return arr
}
fun partition(arr: IntArray, start: Int, end: Int): Int {
var left = start
var right = end
val pivot = arr[(left + right) / 2]
while (left <= right) {
while (arr[left] < pivot) {
left++
}
while (arr[right] > pivot) {
right--
}
if (left <= right) {
arr[left] = arr[right].also { arr[right] = arr[left] }
left++
right--
}
}
return left
}
val sortedList = quickSort(dataList, 0, dataList.lastIndex)
println("After sorting: ${sortedList.joinToString(", ")}")fun quickSort(arr: IntArray, left: Int, right: Int): IntArray {
if (left < right) {
val pivot = partition(arr, left, right)
quickSort(arr, left, pivot - 1)
quickSort(arr, pivot + 1, right)
}
return arr
}
fun partition(arr: IntArray, start: Int, end: Int): Int {
var left = start
val pivot = arr[end]
for (right in start until end) {
if (arr[right] < pivot) {
arr[left] = arr[right].also { arr[right] = arr[left] }
left++
}
}
arr[left] = arr[end].also { arr[end] = arr[left] }
return left
}
val sortedList = quickSort(dataList, 0, dataList.lastIndex)
println("After sorting: ${sortedList.joinToString(", ")}")
병합 정렬 (Merge Sort)
- 하나의 배열을 두개의 균등한 배열로 분할하고 분할된 배열을 각각 정렬한 다음, 이를 다시 합하여 정렬을 완성하는 알고리즘
- 분할 정복의 일종으로, 하나의 큰 문제를 두개의 작은 문제로 분할하여 해결한 다음, 결과를 모아서 문제를 완전히 해결하는 전략이다.

| 시간 복잡도 | - average. worst : O(N log N) |
| 공간 복잡도 | 정렬 과정에서 별도의 추가적인 메모리(임시배열)을 사용하므로 제자리정렬(In-place sort)가 아니다. |
| 안전성 | 안전정렬 |
fun mergeSort(arr: IntArray, start: Int, end: Int): IntArray {
if (start >= end) {
return intArrayOf(arr[start])
}
val mid = (start + end) / 2
val left = mergeSort(arr, start, mid)
val right = mergeSort(arr, mid + 1, end)
return merge(left, right)
}
fun merge(left: IntArray, right: IntArray): IntArray {
val merged = mutableListOf<Int>()
var leftPointer = 0
var rightPointer = 0
while (leftPointer < left.size && rightPointer < right.size) {
if (left[leftPointer] <= right[rightPointer]) {
merged.add(left[leftPointer])
leftPointer++
} else {
merged.add(right[rightPointer])
rightPointer++
}
}
while (leftPointer < left.size) {
merged.add(left[leftPointer])
leftPointer++
}
while (rightPointer < right.size) {
merged.add(right[rightPointer])
rightPointer++
}
return merged.toIntArray()
}
val sortedList = mergeSort(dataList, 0, dataList.lastIndex)
println("After sorting: ${sortedList.joinToString(", ")}")선택 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 선택 정렬(選擇整列, selection sort)은 제자리 정렬 알고리즘의 하나로, 다음과 같은 순서로 이루어진다. 주어진 리스트 중에 최소값을 찾는다. 그 값을 맨 앞에 위
ko.wikipedia.org
잔재미코딩 온라인 강의 사이트입니다
잔재미코딩에서 만든 온라인 강의 리스트를 공유하는 웹페이지입니다.
www.fun-coding.org
버블정렬(Bubble sort) 개념/시간복잡도/Stable/In-place
버블정렬에 대한 이해 - 버블 정렬이란, 인접한 두 원소를 비교해 나가며 가장 큰 원소를 끝으로 보내는 과정을 N-1번 반복하는 알고리즘이다. - 선택정렬과 유사하게, N-1번 부터 1번까지의 자리
maramarathon.tistory.com
퀵 정렬(Quick Sort) | 👨🏻💻 Tech Interview
퀵 정렬(Quick Sort) Goal Quick Sort에 대해 설명할 수 있다. Quick Sort 과정에 대해 설명할 수 있다. Quick Sort을 구현할 수 있다. Quick Sort의 시간복잡도와 공간복잡도를 계산할 수 있다. Quick Sort의 최악인
gyoogle.dev
합병정렬(Merge sort)_개념/시간복잡도/Stable/Not In-place
합병 정렬에 대한 이해 - 합병정렬이란, 하나의 배열을 두개의 균등한 배열로 분할하고 분할된 배열을 각각 정렬한 다음, 이를 다시 합하여 정렬을 완성하는 알고리즘이다. - 합병정렬은 분할 정
maramarathon.tistory.com
'코틀린 > Algorithm' 카테고리의 다른 글
| [Algorithm][Kotlin] LRU 알고리즘 (0) | 2024.11.10 |
|---|---|
| [Algorithm] 동적 계획법 (Dynamic Programming, DP) (0) | 2024.08.20 |
| [CodingTest] 자료구조, 알고리즘, 시간복잡도 (0) | 2024.08.20 |


